Skip to contents

Empirical distribution

Source: R/dist_empirical.R
dist_empirical.Rd

Creates an empirical distribution object from a sample. Assumes iid. samples. with_params should not be used with this distribution because estimation of the relevant indicators happens during construction.

Usage

dist_empirical(sample, positive = FALSE, bw = "nrd0")

Arguments

sample

Sample to build the empirical distribution from

positive

Is the underlying distribution known to be positive? This will effect the density estimation procedure. positive = FALSE uses a kernel density estimate produced by density(), positive = TRUE uses a log-kernel density estimate produced by logKDE::logdensity_fft(). The latter can improve density estimation near zero.

bw

Bandwidth parameter for density estimation. Passed to the density estimation function selected by positive.

Value

An EmpiricalDistribution object.

Details

  • sample() samples iid. from sample. This approach is similar to bootstrapping.

  • density() evaluates a kernel density estimate, approximating with zero outside of the known support. This estimate is either obtained using stats::density or logKDE::logdensity_fft, depending on positive.

  • probability() evaluates the empirical cumulative density function obtained by stats::ecdf.

  • quantile() evaluates the empirical quantiles using stats::quantile

  • hazard() estimates the hazard rate using the density estimate and the empirical cumulative density function: h(t) = df(t) / (1 - cdf(t)).

See also

Other Distributions: Distribution, dist_bdegp(), dist_beta(), dist_binomial(), dist_blended(), dist_dirac(), dist_discrete(), dist_erlangmix(), dist_exponential(), dist_gamma(), dist_genpareto(), dist_lognormal(), dist_mixture(), dist_negbinomial(), dist_normal(), dist_pareto(), dist_poisson(), dist_translate(), dist_trunc(), dist_uniform(), dist_weibull()

Examples

x <- rexp(20, rate = 1)
dx <- dist_empirical(sample = x, positive = TRUE)

y <- rnorm(20)
dy <- dist_empirical(sample = y)

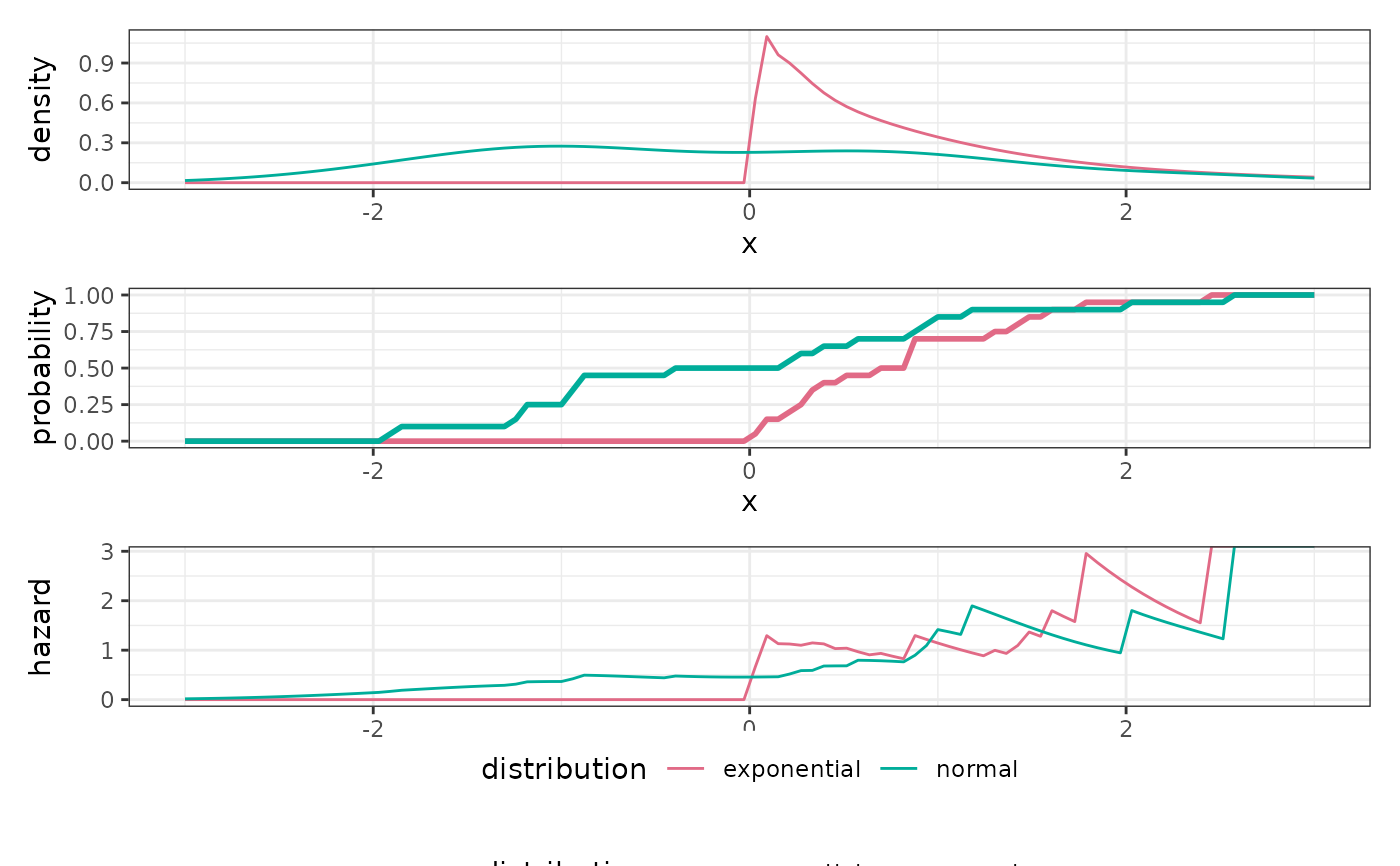
plot_distributions(
  exponential = dx,
  normal = dy,
  .x = seq(-3, 3, length.out = 100)
)