The Generalized Pareto Distribution (GPD)

These functions provide information about the generalized Pareto distribution with threshold u. dgpd gives the density, pgpd gives the distribution function, qgpd gives the quantile function and rgpd generates random deviates.

Usage

rgpd(n = 1L, u = 0, sigmau = 1, xi = 0)

dgpd(x, u = 0, sigmau = 1, xi = 0, log = FALSE)

pgpd(q, u = 0, sigmau = 1, xi = 0, lower.tail = TRUE, log.p = FALSE)

qgpd(p, u = 0, sigmau = 1, xi = 0, lower.tail = TRUE, log.p = FALSE)

Arguments

n

integer number of observations.

u

threshold parameter (minimum value).

sigmau

scale parameter (must be positive).

xi

shape parameter

x, q

vector of quantiles.

log, log.p

logical; if TRUE, probabilities/densities p are given as log(p).

lower.tail

logical; if TRUE (default), probabilities are \(P(X \le x)\), otherwise \(P(X > x)\).

p

vector of probabilities.

Value

rgpd generates random deviates.

dgpd gives the density.

pgpd gives the distribution function.

qgpd gives the quantile function.

Details

If u, sigmau or xi are not specified, they assume the default values of 0, 1 and 0 respectively.

The generalized Pareto distribution has density

$$f(x) = 1 / \sigma_u (1 + \xi z)^(- 1 / \xi - 1)$$

where \(z = (x - u) / \sigma_u\) and \(f(x) = exp(-z)\) if \(\xi\) is 0. The support is \(x \ge u\) for \(\xi \ge 0\) and \(u \le x \le u - \sigma_u / \xi\) for \(\xi < 0\).

The Expected value exists if \(\xi < 1\) and is equal to

$$E(X) = u + \sigma_u / (1 - \xi)$$

k-th moments exist in general for \(k\xi < 1\).

References

https://en.wikipedia.org/wiki/Generalized_Pareto_distribution

Examples

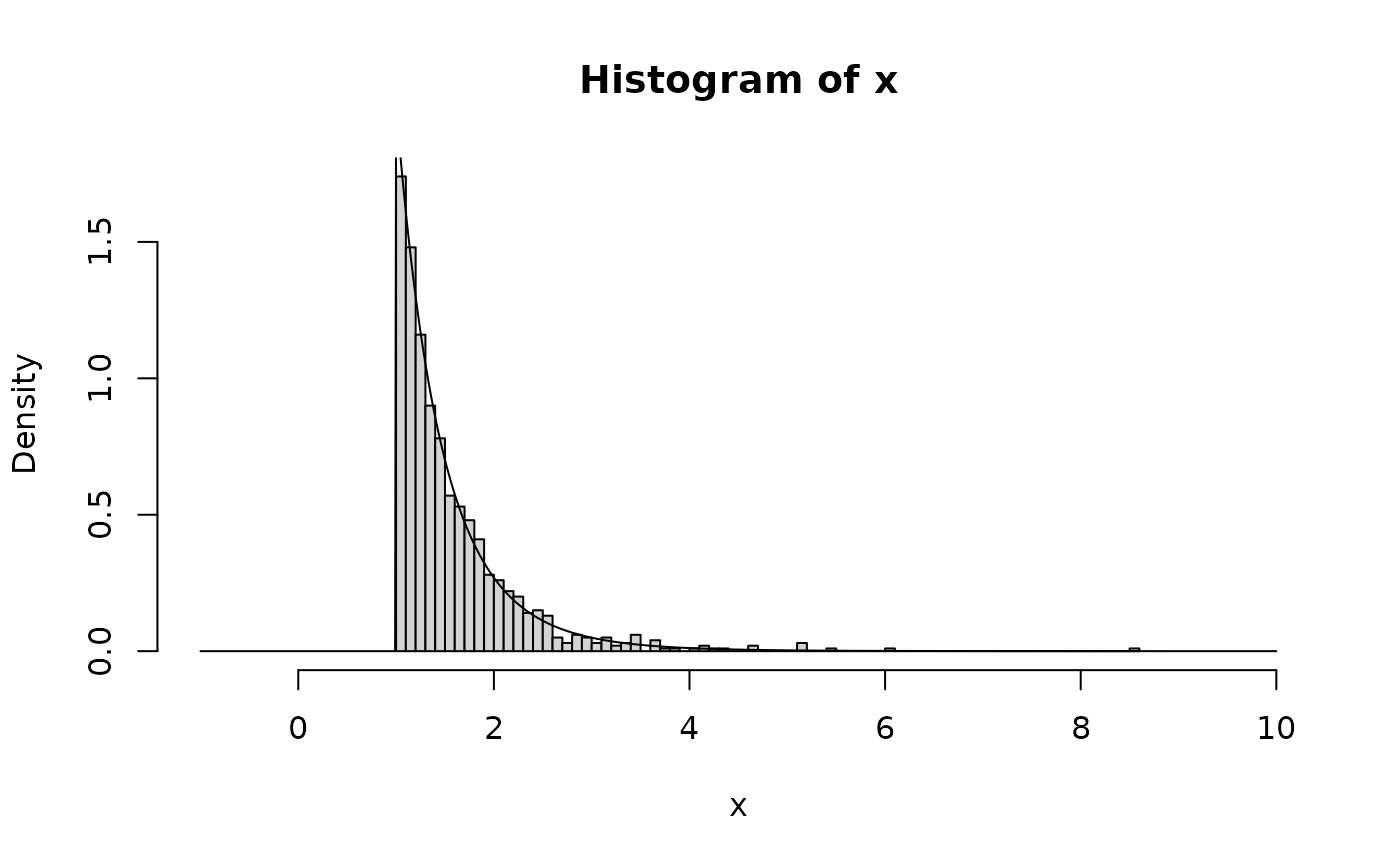
x <- rgpd(1000, u = 1, sigmau = 0.5, xi = 0.1)
xx <- seq(-1, 10, 0.01)
hist(x, breaks = 100, freq = FALSE, xlim = c(-1, 10))
lines(xx, dgpd(xx, u = 1, sigmau = 0.5, xi = 0.1))


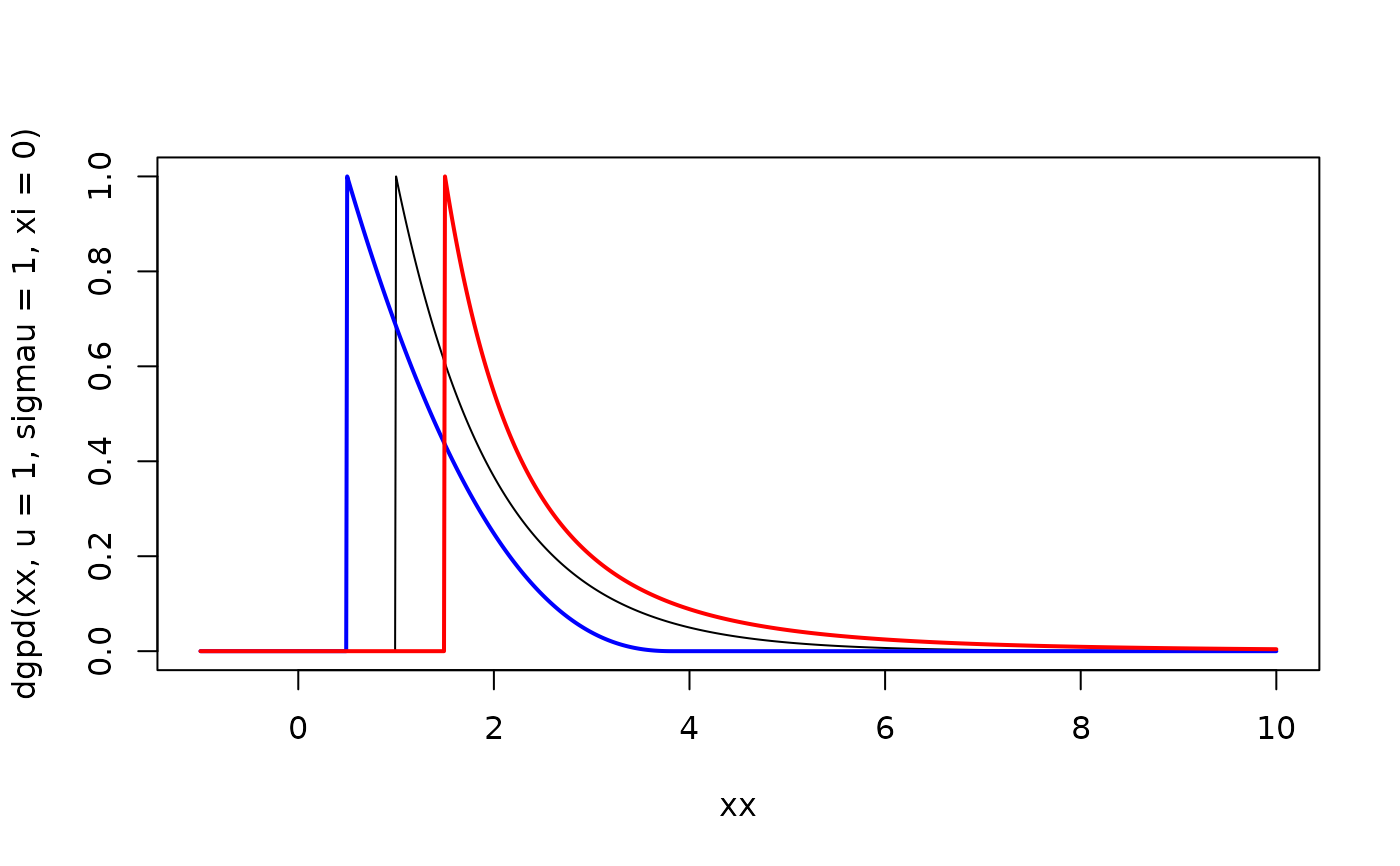
plot(xx, dgpd(xx, u = 1, sigmau = 1, xi = 0), type = "l")
lines(xx, dgpd(xx, u = 0.5, sigmau = 1, xi = -0.3), col = "blue", lwd = 2)
lines(xx, dgpd(xx, u = 1.5, sigmau = 1, xi = 0.3), col = "red", lwd = 2)


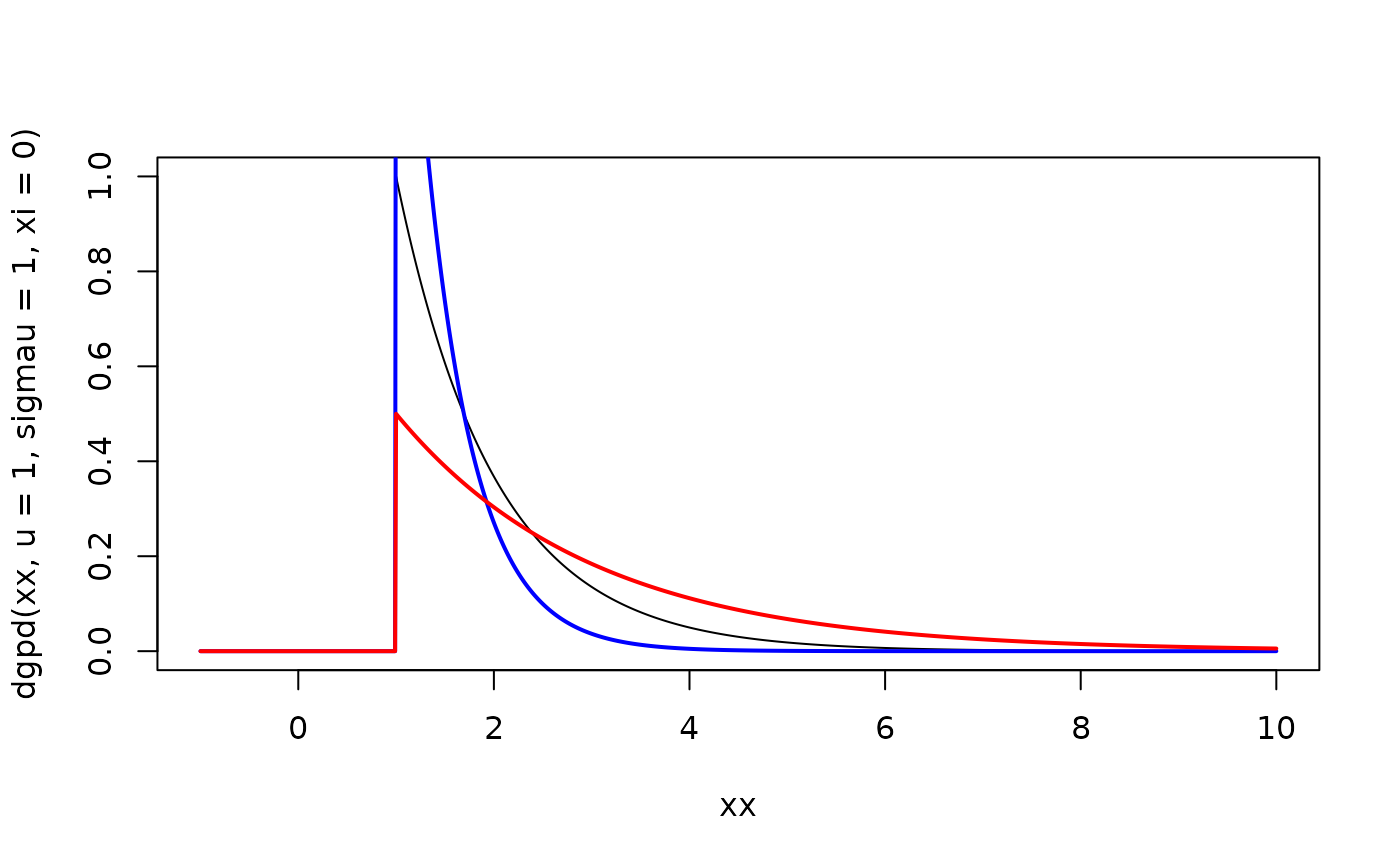
plot(xx, dgpd(xx, u = 1, sigmau = 1, xi = 0), type = "l")
lines(xx, dgpd(xx, u = 1, sigmau = 0.5, xi = 0), col = "blue", lwd = 2)
lines(xx, dgpd(xx, u = 1, sigmau = 2, xi = 0), col = "red", lwd = 2)